,
respectively. These appeared to be reasonable lower limits of larval mortality
which might be expected.U.S. Dept. of Commerce / NOAA / OAR / PMEL / Publications
Survey design. Data from larval walleye pollock surveys of Shelikof
Strait in 1986 and 1987 were examined to set the overall boundaries of the sampling
area used in the present study and to estimate the likely abundances of larvae.
An analysis of these data was used to estimate the number of stations needed
to detect a reasonable minimum mortality rate. A power analysis (Zar
1984), using an estimate of variance of larval abundances in 1986 and 1987,
indicated that, for a power of 0.8 and 0.95, a sample size of 50 stations per
pass would detect overall mortality rates of 0.029 and 0.037 d,
respectively. These appeared to be reasonable lower limits of larval mortality
which might be expected.
A stratified survey design was used for both passes. A stratification scheme for the first survey of the area (Pass 1) was based on prior information. Historically, high densities of larvae have been observed between Sutwik Island and the Semidi Islands (Fig. la). We also expected high densities in the inshore area north of Sutwik Island. Five strata were included in Pass 1 (Fig. la). The 7 strata for the second survey (Pass 2, Fig. lb) were determined from the shipboard counts of the larvae found in Pass 1. The high inshore abundances found in Pass 1 were predicted to move to the southwest with the prevailing current; therefore the Pass 2 survey was extended further to the southwest.
Fig. 1. Survey area for (a) Pass 1 and (b) Pass 2, including station locations and strata boundaries.
The cruise was conducted from the NOAA vessel Miller Freeman between 19 May and 9 June 1988. A grid of stations 9 or 19 km apart was established as described above and refined based on larval surveys of prior years, and from results of egg and larval cruises in April and May 1988. This grid was occupied from 21 to 24 May (Fig. la, Pass 1) and was resampled from 1 to 6 June (Fig. lb, Pass 2). The mean dates of each pass were separated by 12 d.
Three sets of gear comparisons were done -- on 20 May, 30 May and 6 June --
to examine catch rates by fish size for an estimate of larval escapement and
avoidance of gear. The gears tested were a 60 cm bongo net with 0.333 mm mesh,
a 1 m Tucker trawl with 0.505 mm mesh, a 3 m Tucker trawl with 1.5 mm mesh,
and a Methot frame trawl with 2 × 3 mm oval mesh (Methot
1986). This range of gear types and mesh sizes has been shown to catch walleye
pollock ranging from ca 4 to 40 mm standard length (SL) (M. Shima & K. Bailey
unpubl.). Two daytime tows and 1 or 2 nighttime tows were done with each gear
type. Each set of gear comparisons was located in an area of relatively high
(>250 larvae 10 m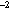
) abundance, and took
ca 24 h to complete. All hauls for a particular set of gear comparisons were
done at the same location.
The first set of gear comparison tows (20 May) indicated that the Tucker trawl
was the most efficient in catching the size range of larvae observed (4 to 15
mm SL). It was therefore chosen as the standard gear for the larval surveys.
Oblique tows were done to a depth of 100 m, as prior work has shown that larvae
are above 100 m at this time of year (Kendall
et al. 1987). The ship's speed was approximately 2 to 2.5 knots. A flow
meter was used to normalize catch for volume filtered. The Tucker trawl was
deployed with the net closed, and a messenger was sent to open the net when
it reached sampling depth. The net was then retrieved at 20 m min.
A subsample of walleye pollock larvae was removed from the cod end and immediately preserved for special studies. This subsample included larvae which were preserved in 95% ethanol for daily growth increment analysis. In order to find areas of high concentrations of larvae for further special studies and to find the boundaries of the larval distribution (to ensure that the complete larval distribution was sampled), a volumetric subsampling method was used on the remainder of the catch to estimate the total number of larvae. The remaining contents of the cod end, aside from larvae removed for special studies, were preserved in 5% buffered formalin. These samples were later resorted for a final count of walleye pollock larvae, which included those that had been removed for special studies.
Analytic methods. The number of larvae per tow was converted to number
of larvae per 10 m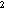
using a standard haul factor
(Smith
& Richardson 1977). Total number of larvae per pass was the sum over
all strata of the stratum mean multiplied by the area of the stratum.
Gear comparisons: For each of the 3 sets of gear comparison tows,
catch rates by larval size interval were compared among gear types to test whether
significant numbers of small or large larvae were missed by the sampling gear,
and to examine catching efficiency by larval size. The number of larvae per
10 m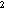 per 1 mm SL interval for each of the gear
comparison tows was averaged by gear type. A Kolmogorov-Smirnov test (K-S;
Zar 1984) was done to assess the difference in catch rates between the bongo
net and the 1 m Tucker trawl.
An analysis of variance (ANOVA) of 1 m Tucker trawl catches was done to test
whether catch rates differed between day and night (indicating gear avoidance).
The catch per 10 m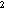 at each survey station was
log-transformed to equalize the variance. The factors in the ANOVA were strata
and day/night. Two strata from Pass 1 were excluded because they contained only
stations done during the day.
Length-frequency and shrinkage: The standard length of 50 walleye pollock larvae per haul (Passes 1 & 2) was measured from a combination of ethanol-preserved larvae, formalin-preserved larvae, and larvae measured before preservation. Larval lengths from each preservative type were combined in order to construct an unbiased length-frequency file. Biases by preservative type were due to selective removal of larvae (by size) for special studies. The number of larvae measured from each preservative type was proportional to the total number of larvae which had been placed in that preservative. Samples from each preservative type were random. Lengths of larvae from different preservative types were converted to fresh (prefixation) lengths using the following relationships:
and
These relationships were derived from experiments [in 1988 and other years; D. Seifert, Alaska Fisheries Science Center (AFSC), 7600 Sand Point Way NE, Seattle, WA 98115, USA, pers. comm.] where fresh length and preserved length were measured on the same fish. Converted lengths were combined into an overall length-frequency for each pass.
Aging: Approximately 15 to 20 fish per station from about 15
stations per pass were aged from otoliths by enumerating daily growth increments
(Yoklavich
& Bailey 1990). Daily growth increments have been validated by laboratory
studies for this species (Nishimura
& Yamada 1984, Bailey
& Stehr 1986). Growth was linear over the size range (4.7 to 18.2 mm)
examined (R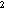 = 0.90).
An analysis of covariance (ANCOVA) was done to test differences in growth over the study period and area. The ANCOVA included length as a dependent variable, stratum as a categorical variable, and age as the covariate, and included an age-stratum interaction term. The analysis showed that the slope of the age-length regression (over the common range, 5 to 18 mm) did not vary significantly among stations over the survey area (p = 0.919). Within each pass, pair-wise tests of the equality of the intercepts (using Bonferroni probabilities; Miller 1981) of the length-age regression among strata showed that within Pass 1, 4 of the 5 pairs of strata tested had the same intercept (p > 0.05), while 1 was statistically different (p <0.05). However, this difference was small and we considered it insignificant. Within Pass 2, the intercepts were the same among strata. Growth rates within each pass were therefore treated as equal.
Mortality estimation: An age-length key (Kimura
1977) was computed for each pass. There were 309 larvae aged from Pass 1
and 249 larvae aged from Pass 2. The elements in each row (q
)
of the key are the proportion of fish in length interval l that are age
a, thus each row is the age distribution for the length interval. Each
element in the matrix is used to estimate the proportion of length l
larvae in the population that are age a. Age and length intervals were
chosen to cover the range of the aged larvae (length ranged from 3 to 22.5 mm,
age ranged from 6 to 62 d). The interval size must be large enough to contain
enough larvae in the sample to produce reliable estimates of the true proportions
in the population. In this application, length intervals of 0.5 mm were used.
Daily ages were desired, but this resulted in too many age intervals for the
number of aged larvae, so age intervals of 3 d were used. Additionally, the
use of age intervals less than 3 d would not be justified as the measurement
error in the aging process was ±1 d.
An age-length key was used for this study rather than an estimated age-length relationship for converting length-frequencies into age-frequencies. This is necessary because fish of a specific cohort may be missing from the population but could be misidentified in the length composition due to the averaging effect of the model. An age-length key preserves the shape of the age distribution present in the aged subsample, which is assumed to be a precise representation of the true age distribution if the aged subsample is unbiased.
The standardized catch of larvae at each station was partitioned into 3 d cohorts based on the length distribution at the station and the appropriate age-length key. Cohorts were defined by the age of the larvae on the mean date of the pass. For example, the mean date for Pass 2 was day-of-the-year (DOY) 155, so a larva sampled on DOY 153 with an estimated age of 22 to 24 d would be assigned to the 24- to 26-d-old cohort, its age on DOY 155. This age adjustment for the day of sampling was necessary because the duration of each pass (5 d) was longer than the duration of a cohort (3 d).
The total number of larvae in each cohort for each pass was computed by summing the estimated cohort totals from each stratum. The cohort totals for each stratum were estimated by averaging the estimated number of larvae from each station in the cohort over stations, then multiplying the average by the total area of the stratum.
where C
= estimated abundance
of cohort a in Pass h; C
= estimated abundance of cohort a in stratum i in Pass h;
C
= estimated no. of
larvae in cohort a per 10 m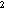 at station
j in stratum i in Pass h; A
= area of stratum i in Pass h in units of 10 m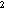
; and N = no. of stations
in stratum i in Pass h.
The variance of the estimated cohort totals has 2 components: the variability about the standardized catch sizes within each stratum and the uncertainty about the age distribution. This uncertainty is due to using an age-length key to estimate the age of the larvae rather than measuring the age of each larva directly. Kimura (1977) estimated variance of an age distribution from an age-length key; however, in the present application, the age distribution variance was complicated by the fact that a cohort is comprised of larvae from different age intervals corresponding to the different sampling dates. Therefore, an estimator for the variance about a total of a range of ages was used (S.J. Picquelle, ASFC, pers. comm.). Covariance between the estimates for a cohort from the 2 passes is assumed to be zero because these estimates are taken from 2 surveys which are statistically independent.
Mortality rates were estimated for each 3 d cohort that was present in both passes. Cohorts represented by very few fish in the age-length key (i.e. very young and very old fish) were dropped from the mortality analysis, as they were suspected of being underrepresented in the catch. The mean dates of the 2 passes were separated by 12 d. An exponential function was used to estimate cohort-specific mortality rates over the 12 d.
where z
= estimated instantaneous
daily mortality rate for cohort a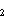; t
– t
= time between
passes (12 d); C
= estimated abundance of cohort a in Pass 1; and C
= estimated abundance of cohort a in Pass 2.
This model was also used to calculate the instantaneous daily mortality rate for the combined 10 April to 16 May cohorts.
The variance of the mortality rate was estimated using the delta method (Seber 1982):
where Var (z) = approximate
estimate of variance about the mortality rate for cohort a; and Var
(C
) = estimate of
the variance about the estimated abundance of cohort a in Pass h
(Picquelle pers. comm.).
The significance of the mortality coefficients could have been tested with a simple t-test, however, the variance of the mortality rate is an approximation. Therefore, the significance of the mortality rate was inferred through the use of a test of the difference in abundance of each cohort between Passes 1 & 2. This was a 2-tailed test where the variances of the abundances were not assumed to be equal and the critical value for the test was a weighted average (Sokal & Rohlf 1981).
Biases to the mortality estimates caused by advective transport into or out of the study area were examined by a model of advection and diffusion developed for this area (P. Stabeno & L. Incze, NOAA, Pacific Marine Environmental Laboratory (PMEL), 7600 Sand Point Way NE, Seattle, unpubl. data). The model is a 2-dimensional (depth-integrated) finite difference model with an imposed velocity field, that contains terms for larval mortality and age-dependence:
where C = the depth-integrated concentration of larvae; t = time;
U = cross-strait horizontal velocity; x = cross-strait axis; V
= along-strait horizontal velocity; y = along-strait axis; K
= horizontal coefficient of eddy diffusivity; Q(a,x,y,t) = the
larval source and sink term (i.e. hatching and mortality); and a = larval
age.
The concentration of larvae was assumed constant normal to the model boundaries [C(x,y,t) = 0]. The horizontal velocities and coefficient of eddy diffusivity (which is assumed constant) were determined using drift buoy and current meter data. The only biological input into this model was an age-dependent mortality which enters via the Q(a,x,y,t) term.
Larval concentrations measured during Pass 1 were used as initial input to the model. The age-dependent mortality used was from Yoklavich & Bailey (1990). The model was run for 12 d with the mean observed current field (as derived from satellite-tracked buoys; P. Stabeno & R. Reed, NOAA, PMEL, unpubl. data). The percent of larvae expected in the region covered in Pass 2 was predicted from the model output. For the mortality estimation, survey boundaries for Pass 2 were adjusted to reflect the area where more than 95% of the larvae were predicted to be by the model 12 d after the mean date of Pass 1.
As an alternative, mortality rates derived from the age composition within each pass were also calculated via catch curve analysis (Ricker 1975) for comparison to those derived from the 2 passes. Assumptions made when using this method are that production of fish of all ages is constant, that mortality rate for all ages is also constant, and that all ages are equally vulnerable to sampling gear. Total mortality rates, over all ages, from the catch curves within each pass were calculated from a regression of log abundance on age:
where C = estimated abundance
of cohort a in Pass h; t
= age of cohort a; 
= intercept for Pass h; z
= estimated instantaneous daily mortality rate for Pass h.
Larval drift: Larval spatial distributions were contoured separately for each 3 d cohort for each pass. These plots were examined for patterns of distribution and for evidence that part of the larval distribution might have been missed in either Pass 1 or Pass 2 (indicated by high concentrations of larvae near the survey boundaries), thereby biasing the mortality estimates. Drift of larvae between Passes 1 & 2 was measured by assuming coherence of 3 major observed larval patch features, and by measuring the net movement of these patches between the passes.
Centroids, a measure of the center of mass of the larval distribution computed by using abundances at each station weighted by the locations of the stations (Kendall & Picquelle 1990), were calculated for all larvae from each pass. Centroid locations were corrected for irregular sampling distribution (with more stations in the inshore areas) by weighting each station location not only by larval density, but also by the area each station represented. Net displacement of the centroids of larval distribution was calculated for the interval between the 2 passes.
The 2 estimates of larval drift (from patch displacement and centroid displacement) were compared to the estimates of upper-water-column movement derived from a satellite-tracked drift buoy that was released in an area of larval concentration near the Alaska Peninsula during Pass 1.
Return to previous section or go to next section